Updated/Decorated

When you have all of your work done for the upcoming week (go me!) it leaves time to do things you really love...like decorating.

I posted about my pong game forevvvvver ago and it's one of my classics and student favorites. After seven years of playing it, students have finally figured out to toss it underhanded. Now that the secret is out, it's gotten a lot easier.

So I figure it was time to up the stakes. And I finally made it look pretty which should surprise no one.

I used shelf liner on the lid from a copy paper box. Then I made cards with different point amounts and taped them to the bottom. I hot glued the cups down and well, just look at it...

...Makes my heart happy.

A couple years back I posted about my teacher tool box that I keep supplies in. I redid them with new scrapbook paper and changed some of the things I was storing.

If you can't tell, I love chevron.

Like a lot.

A LOT a lot.

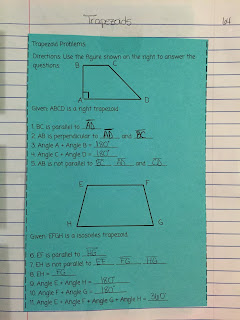
Geometry Unit 6: Quadrilaterals Interactive Notebook

Pg 59-60 You might have seen this RHP on Pinterest which I modeled it after and tried to use the graphic organizer on the LHP to reinforce things we drew. I did not implement this well because students copied it without discussion. For some reason, I thought they would look back and get all this meaning from it when we didn't spend any time creating any meaning. =(

Pg 61-62 These pages came after this activity from Pam to reinforce the different properties of diagonals and then using those properties to solve algebraic problems.

Pg 63-64 I know I found theses somewhere online but don't know where. I don't think they were super useful, I think I was desperate for something to use.

After this I also did interior angle sum and exterior angles but I have no pictures to share.

Here are the files:

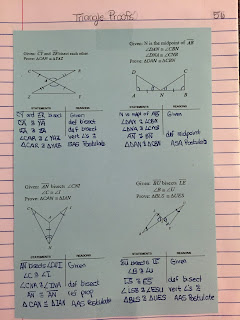
Geometry Unit 5: Congruent Triangles Interactive Notebook

Unit 5: Congruent Triangles

Pg 51-52 Introducing the concept of congruence statements and how order and position matter. LHP using a congruence statement to list congruent parts and a triangle that spins to match the position of the original triangle. RHP matching pictures to the correct congruence statement.

Pg 53-54 These pages are all thanks to Shireen. LHP I turned her worksheet into a foldable for deciding which types of postulate applies and the RHP I printed two to page to fit and students name postulate and write a congruence statement- one of my favorite pages.

Pg 55-56 LHP is a checklist of hints for students to use when writing proofs- I don't know how useful it is. RHP is just example proofs.

Pg 57-58 LHP reminds students of what we know after we prove triangles are congruent in order to remember what CPCTC means and when to use it. RHP very basic examples of CPCTC proofs.

Here are the files:

Linking Cube Towers

This activity was completely stolen from Mary Bourassa's blog post so I will let you go there to read about it and download the file.

The premise is that students will use one color of blocks as their starting value for the tower and a bunch of different color blocks to use as their rate of change. They write a table, graph, and form an equation.

That part went pretty well, once students realized that I was not going to read the directions for them or tell them what to do. {Apparently I waited too late in the year to start teaching freshman about the beauty of reading and following directions.}

Then towards the end when students had to make predictions abut when towers would be the same height or at what step a tower has a certain amount of cubes, it kind of fell apart. I had to give a lot of instruction there when I had hoped that they could work through it without me.

And some who worked it out, didn't make connections to the algebra or the equations. It also seemed that they made no connections to slope, y-intercept, or the meaning of the graph being linear. The activity went okay but they didn't make any of the connections I was shooting for.

I put similar questions on their assessment and ended up not counting them as a grade since only 2 out of 14 students answered correctly.

I noticed at the end of this activity that I was thinking about presenting this activity to my juniors and seniors, just to see that they could do it and make the connections I wanted. I think I was putting blame on the students for not getting what I wanted out of the activity instead of taking responsibility for not scaffolding the activity well enough. I wanted to 'prove' to myself that I was still a good teacher, even if 'these' students didn't learn the way I wanted them to.

Now that it's over, I want to think of ways to make it better as well as more activities where students have to read and follow directions in order to learn something new without me. I've done this many times in the past, but not with 'these' students. Which is why I felt confident that my older students could do it. Instead of blaming students, I put the blame on my lack of quality activities.

Trig Unit 5: Law of Sines and Cosines Interactive Notebook

Unit 5: Law of Sines and Cosines

Pg 49-50 Started this unit with the investigations by Illumination that develop the Law of Sines and Cosines. Then we used these pages to practice the formulas.

 Pg 51-52 These pages cover three cases of the ambiguous case with the SSA postulate. After doing the problems, students cut and paste the correct pictures.

Pg 53-54 Similar to our Law of Sines pages, we developed the formulas and then practiced the Law of Cosines.

Pg 55-56 We practiced word problems by first using the COS diagram (Thanks Meg Craig!) to decide when to use LoC and when to use LoS.

Here are the files:



See my update to this unit this year with area of oblique triangles.

Area of Oblique Triangles

I am pretty proud of myself for this because I modeled it after the Law of Sines and Law of Cosines lessons found on Illuminations. I have to admit, it pretty much all came from my Blitzer Algebra and Trig textbook but I'm still happy that I put it together and am kept lessons consistent throughout the unit.

So here is the 'investigation' where students develop the area formulas:



And next the INB pages we put in our notebooks, inspired by Jennifer Cook's foldable:



Here's what it looks like in real life:

And last but not least, here is the matching powerpoint:



Anybody have an interesting way to introduce or develop Heron's formula?

Digital Answer Keys

...are a god send!

If you have them, you can easily turn boring worksheets into games. Or even simpler, hang the answer key up and let students self monitor their work so you can spend time addressing real questions.

I have turned many a worksheet into a pong game by merely snipping the problem and answer and pasting into a powerpoint.

And of course, it's always helpful to have answer keys for assessments already made.

I have been collecting paper answer keys all year and one of my projects for this summer is to make sure I have a digital version for each one. Even if they are just handwritten, scanning them provides the option to snip and paste those answers wherever I would like. I'm sure this would also come in handy for QR codes and even Kahoot. Kuta is great for this depending on the question type you are looking for.

Such an easy task that can pay off big for you in the long run. Copy and paste are a teacher's best friend.

Not to mention it is great for other teachers when you share a file with an answer key included. =)

Law of Cosines Review Game

This is not much to share but if it helps someone else not have to do it themselves, then I have succeeded. =)

I taught Law of Cosines and the next day used this to practice.

I play a game called pong where students bounce a ping pong ball off a desk into a cup. Each cup is a different color and different point value. Most students are terrible at it because they throw it overhand (I don't know what game they would have learned that from) instead of bouncing it underhand. It frustrates them because they think they will be amazing at it and then it takes the whole class period for them to score even one time.

But it can be used for any game you want. There are 12 questions. Click a number on the home screen. Problem pops up. Click again to show the answer. Click the home button to return to the home screen.

The end.