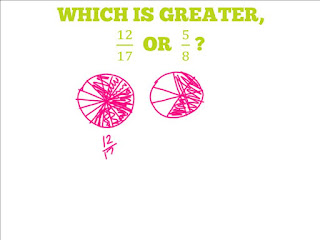8.30.2016
Guys, I'm Killing It
I don't know exactly what gave me my teacher mojo back but I definitely know that last year was my seven year slump.
I've had good things that I've wanted to blog every day but my internet has been lame at home and I'm still so tired every day that I've gotten behind.
Day 1 and I already knew everyone's names.
My biggest class is 18 and my smallest is 5.
I've tried so many new things already: number talks, Google classroom, Google forms, a clothesline activity, asking students to notice things before we start working, introducing growth mindset, using my Plickers multiple times, and my questioning skills have greatly improved.
Here are some highlights from the past two weeks:
Using a beach ball every Monday at the beginning of class- we hit it while we talk about our weekends and we stop when no one else has anything to share. This has been a GREAT way to get energy flowing on a Monday and to get more students talking and for longer amounts of time. And almost every class will ask me about my weekend too- maybe to just keep hitting the ball longer.
I asked our tech person about the possibility of sharing some Chrome books with the two teachers who have classroom sets and she showed up at my door the next day with six that are mine to keep, one per table group. I literally teared up at her kindness.
During my growth mindset discussion with my seniors I kindddddddd of went off on a tangent about being a confident woman and how important it is to make being with yourself a safe place and being successful in the future and etc.....when I finally finished a student said, "Wow, you should be like a coach or something." {I've always wanted to write a book and I think I might have just stumbled on the topic}.
I tweeted about my favorite problem of all time and in my freshman class, the first person to get the correct answer was the student who spent the first week of school telling me how math was not her subject and to please not call on her when she doesn't know the answer. I said "I thought math wasn't your thing and yet you were the first one done." She said, "Well I thought it wasn't!" She worked really hard the rest of the class period.
I was talking to a group of students when one almost let a cuss word slip; she cut herself off and said "This is why you shouldn't make me like you so much- then I talk normal around you." Lol
Number talks have been going well but they really prefer dot talks to anything else so far. Some students are purposely counting them in an unusual order just so they can share their thinking. I've had multiple hands go up to share their thinking and it feels like everyone is comfortable with that.
I feel like it was so easy to just jump right into how I want my classes to run- I already feel like I've known my freshman students for a long time and it's such a testament to how being consistent and building routines and procedures can enhance your classroom culture.
I taught the same piecewise functions lesson that I always teach but I started by asking them to notice things about the function and then notice things about the graph. It seemed like the lesson went so much smoother because they made connections all the way through.
It's only week three I know but I haven't really had to beg people to work; I feel like I have a good mixture of students that helped make this happen.
A few students have made real efforts since last year to change their attitude and effort and it's so cool to see them grow.
I feel so blessed to get to be in their lives year after year and to know them so well that I can see change and growth over time. Also after reading tweets and blog posts, I also feel blessed to be in a school that provides me with all the colored paper {and most school supplies} that I want and that my biggest class size is smaller than most people's small class size.
I still love when students come in and love the way my room smells- I didn't it was so odd for a teacher to buy air fresheners. ;)
A student asked me how much I spend on all of this stuff and I just appreciated that she noticed the extra that I put in.
This was the first year I didn't dread back to school time, the first year I had no school nightmares, and the first year {that I can remember} that I don't have that one class that I'm just dreading.
I can't really explain how my questioning skills have improved but it's like I am self-editing in real time- I'll have my next question on the tip of my tongue and it's like my brain says 'Here's a better idea!" and a more interesting question comes out.
Three lessons that I already had resources for meant I could think deeper about how to present them in a more conceptual way- this is another area I see improvement in myself over time.
I still maintain that Jesus gives me supernatural patience and I can feel the moment I enter into it- helping students one on one I always reach a point where I want to walk away and it's like this supernatural patience washes over me and I just continue like nothing happened.
I don't know why but I think it is so cute when students tell me bye as they leave. It's not every student but it's just endearing.
I've started almost every paragraph with 'I' so far but as hard as we are on ourselves, I think we can all stand to brag on ourselves. One of my gifts is making connections with people and I love seeing that come to fruition- this year feels just like a continuation of last year rather than a new start. Maybe it's not the best thing but I felt like starting school as a tee again- I loved hearing the updates of what all my friends did over the summer and what was going on in their lives.
I feel like finally all of my experience and ups and downs and talents and strengths and weaknesses are coming together and I'm approaching the ever elusive peak of 'actually knowing what I'm doing'.
My career is on an uphill swing and that is definitely ONE GOOD THING.
Tags:
#Blaugust
8.27.2016
Plan With Me...Infinite and No Solutions
So I'm planning this lesson for the upcoming week and I have 3 slides that I feel like are a good start. I'm just about to tweet them out and ask what I can add to them when I decide to check the MTBoS search engine first. I land on this great blog post about using Desmos to check answers after combining like terms by graphing.
And instantly my lesson just got better. I get to use Desmos for the first time with my freshman and we are just beginning!
Here's a general outline and my thought process.
I will ask students to share out some answers and I will write them on the board. I will have one chrome book per group of three students and ask them to each take turns typing in an expression from the board (I'm thinking 6 so each student types in 2 and purposely include wrong ones). But what if I don't get very many answers?
I will ask them what they notice as they type in each equation.
We will discuss the connection between the expression and the line.
Next:
I will ask students to prove me right or wrong. I'm thinking I'll have to explain that they either need to solve for x or plug in random values and see what happens. Some kind of work will happen which will lead us to graphing it in Desmos and seeing if it is the same line or not.
Third:
Some kind of work happening, either with Algebra or Desmos leading up to the fact that they graph two parallel lines which have no intersecting solution and how they simplify to the same slope with different y-intercepts.
Is that it? Now we just practice?
What are some good questions I can ask? What needs to go in their notes?
And instantly my lesson just got better. I get to use Desmos for the first time with my freshman and we are just beginning!
Here's a general outline and my thought process.
I will ask students to share out some answers and I will write them on the board. I will have one chrome book per group of three students and ask them to each take turns typing in an expression from the board (I'm thinking 6 so each student types in 2 and purposely include wrong ones). But what if I don't get very many answers?
I will ask them what they notice as they type in each equation.
We will discuss the connection between the expression and the line.
Next:
Third:
Some kind of work happening, either with Algebra or Desmos leading up to the fact that they graph two parallel lines which have no intersecting solution and how they simplify to the same slope with different y-intercepts.
Is that it? Now we just practice?
What are some good questions I can ask? What needs to go in their notes?
Tags:
#Blaugust,
Algebra I Lessons
8.20.2016
First Days 2016-2017
I was not ready. I spent my last few days getting my classroom ready and not preparing actual activities. This should have been an 'easy' week for me since it's the only time I can get away with doing the same thing every hour. Instead I didn't go to bed earlier than midnight all week. =( Definitely making a check list so this doesn't happen next year.
Monday
Today we did Mental Math Monday and got our binders ready: dividers, tabs, names on the spine, pencil bags, new pencils, and dry erase markers. We folded our name tents; I loved having students write to me every day. The name tent part was not really necessary since we are so small and everybody knows everybody. Next year I might not use an actual name tent. It also took me up to an hour and a half each night too respond. I would say it is worth it but I definitely couldn'tdo it all year.We did our first number talk!
Tuesday
1-100 task making groups work. The kids LOVED it!! In between rounds we discussed strategies for working together and improving their times.
Wednesday
We started with our Work It Wednesday problem, how can you arrange 8 8's to add up to 1000? From there I showed them pictures from the previous day's 1-100 task.
They could not believe that I took pictures! Not a single student in any class noticed I was taking pictures. Not even in a class of 5! They have already asked to do it again. My best group made it all the way to 91 and two groups made it to the 80's. We reviewed the group work strategies and from there we went to Sarah's Broken Circle task. This only took 2-3 minutes since my students were in groups of 3. We finished the day by setting up our INBs.
Thursday
Thursday are my designated day for number talks and it started out rough. Read more here. We again used Google Classroom to open a pdf of my syllabus. I tried Brigid's idea of doodle notes using this doodle syllabus. I still have mixed feelings about this. My artistic students really appreciated it. The students did agree that taking notes from the pdf was better than listening to me talk the whole time. But most of these students have had me for years and know my policies and procedures. More than one person asked why we were doing this and most people didn't even get it finished in a class period because they spent so much time doing what I asked...doodling! I can see it working much better in a lecture heavy class but thankfully, I am heading in the opposite direction of that.
Friday
We ended the week by taking our end of course exam which will be given again in December and May. I spent my time making answer keys and updating my spreadsheet data.
Comparing the first administration last year to this year
Algebra I 15% to 24%
Geometry 18% to 20%
Algebra II 16.5% to 24%
Trig 30% to 19%
I'm using new exams except for Trig so those numbers basically mean nothing but I like that they are moving up. Except what the heck happened in trig?
I'm so glad that thanks to my blog, I have a record of everything I've tried during the first days of school. If you teach in a small school, you know you can't repeat activities until four years have passed. Check out my first days tag if you need more ideas!
Tags:
#Blaugust,
First Days
8.19.2016
My First Number Talk
I was inspired by Sara Van Der Werf's post to finally start doing number talks. I haven't read any of the books yet so forgive me if I'm screwing this up.
It took me three days of number talks before I realized I should start saving these pictures.
They are pretty terrible but I'd like to have a starting point to look back at.
The first two days were counting items in a picture so when I threw this one at them, I realized maybe a fraction problem was not the best one to use first.
We had a rough start but there was about one interesting answer per period so all was not lost.
A lot of them chose 5/8 because they said they learned that the smaller fractions are bigger pieces.
I'm really trying to put the emphasis on how we are thinking about things over right answers.
I also used Sara's name tent idea and more than one student wrote that they liked how we were learning about different ways to think and that they appreciate me letting them be creative.
Be still my heart.
It was much easier to get them to talk about counting dots and footballs but I'm not giving up!
Suggestions appreciated.
Tags:
#Blaugust
8.18.2016
Pharaohs

Things I want to instill in my students or that I hope they 'inherit' from me and my classroom!
P-persistence. Let's get it right and get it done!
H- happiness. I'm really working on two things: to operate out of love and to let life be on my lips. How can I speak life, love, and happiness each day to my 90 students?
A- assertive. Learn the difference between aggressive and assertive. Know how and when to stand up for yourself and others. Learn how to not back down graciously.
R- resilient. You wouldn't believe the things that four of my students in particular are facing this early in the school year. I hope they see in me the 'fighting spirit' to show up every day and do hard work well.
A- attitude. As we learn together about growth mindset, I want to teach them the importance of their attitude and how it sets the tone of each day and the future.
O- original. I think I am pretty good at standing out and being unique. Hopefully my students take away that it is okay to have strong passions and interests and to put them on display.
H- honor. I'm trying my best to start off honoring the different ways of thinking my students have, honoring their identity by asking them to share it, and honoring the important of our relationship by building it.
S- spirit. Take pride in who you are and where you are from. If it's not the best place, then try making it better. Give back. Be successful and share how you got there.
Pharaoh Pride!
Tags:
#Blaugust
8.12.2016
#DITL Back to School! Year 8
I don't count today as our first day because I only saw my kids for five minutes per period. But this was one of the best starts we've had and an all around positive day so you know I have to share.
The day started with the Principal giving updates to the students for about 20 minutes. Then students were released to their classes for 5 minutes each.
This was enough time for me to have students write down their birthdays and favorite candy. I gave them an address label with my Remind number and code. I asked them to get composition notebooks and then I said good-bye!
I asked my freshman class how many of them liked math and none of them raised their hand. I !asked them how many were good at math but didn't like it. No one. I asked them if we could all agree to think positive and that this is going to be a good year of math class. All smiles and head nods. So now it is my personal mission to ask that question at the end of the year and have a majority of the hands go up.
We rotated through all of our classes and then around 9:30 we went to the gym. A student group had some cute games planned but it wasn't super organized. Middle school students had a blast and most of the high school sat on the bleachers and talked. We were there until lunch at 11:30 which was a little long considering we are having air conditioner problems but I made my way around talking to students.
It just felt so nice to be reminded of relationships I've been building for years and the comfort of being surrounded by students I know and I like. I have no classes I'm dreading this year. I spent most of the day smiling and chatting with students and that was just enjoyable!
We had a 12:00 dismissal and then a Google training from 12:30-2:30 which means we also had an hour lunch.
I really love having Back to School night on Thursday and an early dismissal Friday.
Have a great weekend!
Tags:
#Blaugust
8.11.2016
#DITL Back to School Night
My day did not start out very positive. Nobody likes their Teacher Institute to start with the principal reading a 22 point packet out loud word for word of new rules and expectations.
But that is not what I came to write about.
We revamped our Back to School Night and I really enjoyed it so I wanted to share with you. It started at 5:00 where students get their schedules in the lobby and sign up for door prizes. Then they travel around to each classroom and have their teachers sign their schedule. Showing your schedule with all the teacher signatures earned you ice cream in the cafeteria.
Students were in the gym doing face painting and hosting sign up sheets for clubs. This was also the time for students to find their locker, test the lock, etc.
In the library there were videos from last school year playing on a loop.
At 6:30, everyone returns to the gym where the Principal speaks about announcements and updates.
Then names were pulled for door prizes and that wrapped up the night!
If only the air conditioning worked correctly...
I was surprised to see a large group of people in the lobby at 5:00 on the dot.
Only one student I talked to today told me they didn't like math!
Our community 4H group donated Back to School baskets for us- so thoughtful!
I went home feeling energized which is a lot better than the day began.
I can't explain the growth I've experienced since January...or why. But there has definitely been a shift. I have a lot of things to do and get ready still but I'm not overwhelmed. I'm going to take it a day at a time- and it's going to be fine! I'm doing good work. I'm also doing good work to sustain my energy levels. My students deserve the best Ms. Miller I can be right now- not the best Ms. Miller I will ever be.
My motto for the year is 'Add good things to the pile- no more starting over!"
But that is not what I came to write about.
We revamped our Back to School Night and I really enjoyed it so I wanted to share with you. It started at 5:00 where students get their schedules in the lobby and sign up for door prizes. Then they travel around to each classroom and have their teachers sign their schedule. Showing your schedule with all the teacher signatures earned you ice cream in the cafeteria.
Students were in the gym doing face painting and hosting sign up sheets for clubs. This was also the time for students to find their locker, test the lock, etc.
In the library there were videos from last school year playing on a loop.
At 6:30, everyone returns to the gym where the Principal speaks about announcements and updates.
Then names were pulled for door prizes and that wrapped up the night!
If only the air conditioning worked correctly...
I was surprised to see a large group of people in the lobby at 5:00 on the dot.
Only one student I talked to today told me they didn't like math!
Our community 4H group donated Back to School baskets for us- so thoughtful!
I went home feeling energized which is a lot better than the day began.
I can't explain the growth I've experienced since January...or why. But there has definitely been a shift. I have a lot of things to do and get ready still but I'm not overwhelmed. I'm going to take it a day at a time- and it's going to be fine! I'm doing good work. I'm also doing good work to sustain my energy levels. My students deserve the best Ms. Miller I can be right now- not the best Ms. Miller I will ever be.
My motto for the year is 'Add good things to the pile- no more starting over!"
8.10.2016
#DITL August 10th, 2016
9:00 AM Woke up....second to last day to sleep in. =(
10:15 AM Got to school to finish decorating my classroom. Tomorrow is a half day teacher institute from 1-5 and then Back to School Night from 5-7.
Things I accomplished today:
- Cleaned all 6 carts and drawers and put new labels on each drawer (120 drawers)
- Attached new labels inside plastic bins to put in the cart
- Took my pentaminoes, tangrams, and counters into ziplock bags for each cart
- Refilled the cart with supplies
- Finished my Instagram/Milligram bulletin board
- Decorated my door with my lovely chevron stickers
- Rehung my chevron borders around each whiteboard (I'm never taking them down again!)
- Cut out balloon and star shapes on our die cut machine for student birthdays
- Printed out my Plicker cards
- Took the chairs down
- Printed new number placards for each group of desks
- Took down streamers and paper lanterns that I didn't want anymore
- Finished hanging my 'custom' wall clock
- Changed three bags of trash
- Swept the floor
5:15 PM Got home and made dinner; changed clothes and went shopping
Shopping included MORE classroom stuff:
- Wal-Mart: (plastic unit tubs, washi tape, air fresheners, and groceries)
- Aldi (sugar and biscuits lol)
- Walgreens (pictures for my bulletin board)
- Hobby Lobby (light switch covers, silver hanging decorations, foam letters, scrapbook paper, poster board)
- Dollar Tree (plastic bins and baby washcloths for dry erase markers)
- Target (washi tape for binders)
- Staples (my fave green Staedtler pencils)
- Chinese food for a celebratory lunch tomorrow
- Half price shakes at Sonic since I never ate lunch
10:15 Then because I'm a crazy person I went BACK to school to finish some things so I won't be rushed tomorrow
- Rehung my diploma frame that fell and broke
- Hung up my pictures from Walgreens
- Added the baby washcloths to their labeled white bins
- Added scissors labels to their bins
- Hung up the silver hanging decorations
- Set up the air fresheners
- Switched out the light switch cover
- Put out my pencils in my pencil holder
11:30 Finally home. Unload my crap and pick out my outfit for tomorrow. I always like to dress up more for Back to School Night since I look younger. Got everything ready for tomorrow because I hate mornings- even though I don't have to be at school until 1:00, I don't want to get up any earlier than 9:00 and I don't want to be rushed.
And that's a normal day for me- I do crazy things at crazy times all in the name of creating!
I got 12,354 steps today and walked 5.48 miles. I also drank 64 ounces of water.
8.09.2016
How To...Teacher Assessment
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
Again, let me just say that assessment is not something I claim to be any type of expert at. I steal most of my assessments/questions, I don't feel great about the way I grade, etc etc.
But the least I can do is try new things and talk about them.
So here goes!
But the least I can do is try new things and talk about them.
So here goes!
- Class Discussion: This doesn't happen often or well in my classes, tbh. Mostly students asking me questions and me asking them questions- not much 'discussing'. I really like the idea of using controversial words like always, sometimes, never, best, and worst to spark debate among students. That feels like something I can try.
- Desmos: So far I've only used activity builder for some investigations but it's great for formative assessment because I can see all student responses at the same time or individually.
- Feedback Quiz: link here
- Kahoot: Students LOVE Kahoot but unfortunately iPads don't. I've only used them for formative assessment, more like practice but they definitely inspire the kids to try harder. Time limits are the only drawback for me but I like that there are so many public Kahoots that I can use and that creating my own is easy.
- Participation Quiz: link here
- Plickers: The students also LOVE plickers and they always point out to me that we didn't used them enough...like once or twice a year. But behold, thanks to Jonathan Schoolcraft, we will now use them EVERY Friday for Which One Doesn't Belong. Hooray!
- Quiz: Just your standard quiz. I quiz over every concept but considering combining 2-3 concepts per quiz. Although I always have less grades in the gradebook than anyone else considering I only grade quizzes and tests. Hmm...
- Self-Check Quiz: link here; I read about this years ago and it seems to fit feek with self-quizzing concepts mentioned in Make It Stick.
- Unit Test: enough said
- Whiteboard Practice: I mostly use this in my smaller classes which is not awesome but there is something magical about it; students just automatically teach each other or self-correct which is great formative assessment
8.08.2016
How To...Self and Peer Assessment
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
Thanks to mathbythemountain for suggesting this post; after my last post, she asked me to explain each activity.
So here goes! Let me first say....I haven't done any of these and some of them I just learned about this summer.
Self-Assessment:
Peer-Assessment:
Thanks to mathbythemountain for suggesting this post; after my last post, she asked me to explain each activity.
So here goes! Let me first say....I haven't done any of these and some of them I just learned about this summer.
Self-Assessment:
- Brain dump: link here; although it's pretty self-explanatory. I'm thinking of doing this for the first five minutes of study guide day
- Circle Graph Reflection: blogged about here with an INB download
- End of unit summary INB sheet: blogged about here with an INB download
- Reflection question on quiz/test: inspired by Pam Wilson and mentioned in my "Make it Stick" post, I also read about this in Mathematical Mindsets. Seems really easy to implement and useful for both students and me, and apparently students can be very accurate at it.
- Rubric: this is pretty generic and I don't have any examples to share but it could be used for any assessment or project
Peer-Assessment:
How To...Self and Peer Assessment
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
Thanks to mathbythemountain for suggesting this post; after my last post, she asked me to explain each activity.
So here goes! Let me first say....I haven't done any of these and some of them I just learned about this summer.
Self-Assessment:
Thanks to mathbythemountain for suggesting this post; after my last post, she asked me to explain each activity.
So here goes! Let me first say....I haven't done any of these and some of them I just learned about this summer.
Self-Assessment:
- Brain dump: link here; although it's pretty self-explanatory. I'm thinking of doing this for the first five minutes of study guide day
- Circle Graph Reflection: blogged about here with an INB download
- End of unit summary INB sheet: blogged about here with an INB download
- Reflection question on quiz/test: inspired by Pam Wilson and mentioned in my "Make it Stick" post, I also read about this in Mathematical Mindsets. Seems really easy to implement and useful for both students and me, and apparently students can be very accurate at it.
- Rubric: this is pretty generic and I don't have any examples to share but it could be used for any assessment or project
Peer-Assessment:
8.07.2016
How To...Implement Activities
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
Thanks to mathbythemountain for suggesting this post; after my last post, she asked me to explain each activity.
So here goes!
Activities:
- Dry Erase Practice: my students can write on their desks with dry erase markers so I guess you could just call this desk practice. If I have problems prepared, then they work it on the desk and I show the answer. If I don't, then I walk around and look at their work, Or both.
- Task Cards: these are kind of popular now but basically they are problems printed individually on cardstock. I set them on the whiteboard ledge and students or groups come get one card and work it and then return it. Each group should only have one card. Sometimes the cards have answers on them so they can self-check. Sometimes I walk around with an answer key.
- Investigation: for me, this is basically a scaffolded activity that leads them through new instruction. It usually involves a lot of questions, maybe some color coding, maybe some matching, sorting, or calculator directions.
- Desmos: So far I have only used Activity Builder, which is amazing, but over the summer they introduced marble slides and card sorts so I can't wait to use those. Desmos is also great for verifying things with graphs, showing visuals, and introducing transformations.
- Card Sort: these are my favorite of all time and I plan on blogging a 'how to' post about creating them. Basically, if there is something you know students mix up or something they never notice, make a card sort out of it. Ask them to sort the pieces into groups and explain how they sorted. Then give them hints until they find it such as: you should have four groups, each group should have the same amount, etc. SO much more meaningful than you just telling students to look for or pay attention to something- let them discover it on their own.
- Grudge Ball: link here
- Row Game: link here
- Four in a Row: link here
- Triples: usually a set of 15 problems, students in pairs/groups work them out and then at the end they sort into 5 groups of 3 that have the same answer. If they can't find three cards with the same answer, they work together to find their mistakes
Activities that Involve Movement:
- Chalk Talk: link here
- Centers/Stations: students rotate to stations that focus on different topics; answer key to previous station provided after rotating; usually used to review.
- Cornhole Review: link here
- Gallery Walk: link here
- Hedbanz: link here
- Pong Review: link here
- Scavenger Hunt: link here
- Speed Dating: link here
- Trashketball: tape a line on the floor some distance away from the trash can and set out a ream of paper. Students work in groups, everyone works the problem, the group answer that is correct sends one person to shoot. Make up your own rules. I put tape for 2 and 3 pointers. If they don't get the problem correct then they don't get to shoot.
- Vertical Whiteboards: link here
Next up I will explain the assessments mentioned in my previous post. Thanks again Audrey!
8.06.2016
How To...Create a Pacing Guide
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
I'm not going to claim to be an expert in any of these 'how to' posts but I've made quite a few pacing guides and I can at least explain my thinking behind it.
Here is my Algebra I rough draft. Look at it first so that I can break down each decision.
First of all, I want a clear list of topics that I plan on teaching. I want those nestled inside cozy little units. I want a specific number of units that spans the course of a year.
I want these things so I can break them down into small, manageable chunks. I will be starting my eighth year of teaching and to be honest, I usually get about halfway through my pacing guide. That's pretty terrible.
I've just decided: no more starting over!!! I want to focus on adding.
I've started with Algebra I. There are 12 units...which means 3 units per quarter which means 3 weeks per unit. I have 6 or less skills per unit which means 2 skills per week. This is the goal I'm shooting for while knowing that some units will go faster or slower than I predict, the weather will mess up my good intentions several times, and instead of getting upset, I will focus on getting farther and farther along in my pacing guide each year.
I also align my pacing guide to the final exam or end of course exam. This means that next to each skill, I put the question number from the exam that corresponds to that skill. This way at the end of the year, I have a list of each question that students *should* be able to do (since I never get through everything).
This year I added activity structures to check off, mainly because I want to see how often I use certain activities and I want to make sure I include movement more often.
I also included the mathematical practices because I've never done a good job at focusing on them.
Reflection, seld-assessment, and peer-assessment came up a lot in my reading and at TMC this year so I added those sections as well. As you can see, this is a weakness of mine since I have very few ideas to attempt.
I put a 'notes' section at the bottom because I'm trying to get better at reflecting.
For next year, I would like to add vocabulary words, good questions, and prerequisite skills. I will try to add those things along the way so that next year: no more starting over! Hopefully I will remember to update this post in the next month or so with *this year's* final draft.
Oh, and the color strip at the top of each page will be color coded for each course and to that course's INB...of course.
This will also be a great tool to include in my teacher evaluation binder!
What else would you include in a pacing guide that will help you focus? What are some of your favorite strategies for self and peer assessment?
Tags:
Evaluation,
How To
8.05.2016
Classroom Instruction from A to Z
Classroom Instruction from A to Z
Barbara Blackburn
It isn't the strategy- it's how you use the strategy that makes a difference.
My goal is to give them information and let them internalize and give it back; not just force-fed info and make them regurgitate it. I want to give them an opportunity to internalize and express [their learning].
If they are allowed to choose how they will show that they understand the content, many students will invest more time and effort in the task.
Start with one idea and build on your success.
"Learning and teaching is messy stuff. It doesn't fit into bubbles." -Michele Forman
Think of data analysis like a triangle: classroom performance and standardized test scores should be evaluated together with a third data point, your teacher judgment.
Data shouldn't replace your judgment; it should help you make decisions.
Our students are not in their final state when we are teaching them.
The word but can serve as a red light or a stop sign for progress, The word and is like a green light.
Your language reflects your beliefs, and your students follow your model. If they hear you using words as an excuse, so will they.
Give students your BEST: belief, encouragement, support, time
Many students do not have a vision of anything more than where they are right now. You can help them create a vision for themselves through your words, actions, and activities so they they support each other.
"Students learn over half of what they know from visual images." -Mary Alice White
If your form of delivery isn't working, then find a different way to deliver it.
Rigor is not just about difficulty. Rigor is also about helping out students learn to critically think about their learning.
Complexity isn't about doing more work, it's about doing less drill and practice and more higher-level thinking activities.
Allowing students to take a zero reflects lowered expectations. It permits a student to get by without actually doing the work and says to the student, "You don't have to learn this."
Less is more. Give students small amounts of focused work that requires them to apply knowledge and evaluate information.
Our mode of instruction says, "Trust me. I know where we are going, so you don't need to." But students don't always respond positively to that approach.
Effective homework can be completed independently with minimal and appropriate support. If the assignment is too difficult, students are more likely to ask someone else to complete it for them.
"The test of a good teacher is not how many questions he can ask his pupils that they will answer readily, but how many questions he inspires them to ask him which he finds it hard to answer." -Alice Wellington Rollins
As you create questions for your students, remember to build in questions that are open ended, those that have more than one answer.
There are three types of reflection for students: reflecting on what they have learned, reflecting on how they learn, and reflecting on their progress.
During "Three Alike", she writes three words on the board or overhead projector. Students then have to explain what the words have in common.
I shuffle playing cards and each student takes one. While they are taking their cards, I make up the rules. Find your group by matching either the suit, the number, or picture. I prepare the deck ahead of time so that I will have the correct number of cards that will create the desired number of groups.
Just because we do something a lot doesn't mean it works.
Tags:
#Blaugust,
Book Excerpts
8.04.2016
How To...Mathematical Mindsets: How Do I Start?
In my own personal effort to #ExpandMTBoS, I'm starting a new category of blog posts called 'How To' so I can share the strategies behind the resource. I hope new and veteran teachers alike can find something useful. Click on the tag to the right for more posts!
If you're like me, the last five posts were probably overwhelming.
Part 1 {here}
Part 2 {here}
Part 3{here}
Part 4 {here}
Part 5 {here}
Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching
Jo Boaler
There's a lot of things to change, fixm and improve. I tried to break this massive shift to my brain into categories of practical things to do.
Easy: things I can do from day one this school year with no prep
Medium: things I can do in the next couple of months or with some prep
Hard: things to think about this year and plan to do over next summer
Easy
- Ask students to think visually first
- Ask students for the different ways they see and solve problems
- Ask students to look for patterns, similarities, and differences
- In every math conversation, ask students to reason, to explain why they chose particular methods and why they made sense.
- Honor hard work and the struggle over effortless achievement
- Think of all the ways to be mathematical. No one is good at all of these ways of working, but everyone is good at some of them.
- Classroom mantra/poster: Always give help when needed, always ask for help when you need it.
- Do not include early assignments {review?} from math class in the end-of-class grade .
- Do not include homework, if given, as any part of grading.
- Honor student thinking- say, "incorrect but helpful"-there is always some logic there.
- When students want me to tell them how to do a problem say, "Do you want my brain to grow or do you want to grow your brain today?”
- Praise people for having good thinking and for being accomplished, learned, hard working, and persistent; not being smart or fast or for effortless achievement
- To take student thinking deeper say, "You may know a rule for solving this question, but the rule doesn't matter today, I want you to make sense of your answer, to explain why your solution makes sense."
- Teachers can encourage students to use intuition with any math problem simply by asking them what they think would work, before they are taught a method.
- Tell students, "I am not concerned about you finishing math problems quickly; what I really like to see is an interesting representation of ideas, or a creative method or solution."
- Ask students to draw connections between concepts in mathematics when working on problems. Encourage students to propose different methods to solve problems and then ask them to draw connections between methods, discussing for example, how they are similar and different
- Ask students to play the role of being the skeptic; explain that they need to demand to be fully convinced. Students really enjoy challenging each other for convincing reasons, and this helps them learn mathematical reasoning and proof. When students act as a skeptic, they get an opportunity to question other students without having to take on the role of someone who doesn't understand.
- Offer all students high-level math content and believe they can do it
- "One of the greatest gifts you can give to your students is your knowledge, ideas, and feedback on their mathematical development, when phrased positively and with growth messages".
- For definitions, give nonexamples and barely examples instead of perfect examples
- Introduce and build a growth mindset!
- Introduce the headache before the aspirin
- Replace class lectures with instructing reporters who go back and instruct their group.
- Participation quizzes! {Yay Sam!}
- Put student questions on posters,
- Always allow students to resubmit any work or test for a higher grade {I already do quiz retakes but I let students use their notes on tests. Should still allow them to redo tests as well?}
- Take students' ideas and make incorrect statements for the students to challenge
- Instead of asking students to simplify ask students to find all the ways they can represent that are equivalent.
- Tell students what they should know and let them reflect on how much of it they know. Frequently.
- Self and peer-assessment {"Questions that ask students to think about errors or confusions are particularly helpful in encouraging students' self-reflection, and they will often result in the students' understanding the mathematics for the first time."}
- Number Talks
- Ask students to compare and choose methods to problem solve
- Grade multidimensionally
- Give group tests and randomly choose one paper from the group to grade.
- Learn more about Assessment for Learning, A4L
- Do not use a 100-point scale.
- Give diagnoistic comments instead of grades. "The students receiving comments learned twice as fast as the control group, the achievement gap between male and female students disappeared, and student attitudes improved."
- Study after study shows that grading reduces the achievement of students. Share grades with school administrators but not with the students.
- Give students rich mathematical tasks that are low floor, high ceiling
- Open up the task so that there are multiple methods, pathways, and representations.
- Include inquiry opportunities.
Do you feel better now, seeing that the easy section has the most things to do?
Did you notice that most of them include the verbs ask, tell, show, say, show, think, honor, encourage? Those are all forms of talking and I don't know about you, but I am pretty dang good at that.
Look how we can make great change with small changes in our words and demeanor. I am encouraged that there are so many positive things I can do for my students RIGHT AWAY.
Did you notice that most of them include the verbs ask, tell, show, say, show, think, honor, encourage? Those are all forms of talking and I don't know about you, but I am pretty dang good at that.
Look how we can make great change with small changes in our words and demeanor. I am encouraged that there are so many positive things I can do for my students RIGHT AWAY.
Hooray.
All day.
8.03.2016
Mathematical Mindsets: The Highlights {Part 5}
This book I would say has changed my thoughts on math, teaching, and teaching math more than any other I've read in my seven year career. I will recommend it and link it forever. I will have to post my highlighted notes from it in several posts because no one would ever scroll through all of it otherwise! There is just so much to process and that I will need to read over and over again- so many opportunities for growth and change!
It's only $10.71 for the paperback and $7.99 for the Kindle version. You NEED this book. But until you get your own, this should be enough to make you want more.
Enjoy!
Part 1 {here}
Part 2 {here}
Part 3{here}
Part 4 {here}
Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching
Jo Boaler
Chapter 9: Teaching Mathematics for a Growth Mindset
I believe in every one of them, that there is no such thing as a math brain or a math gene, and that I expect all of them to achieve at the highest levels. I love mistakes. Every time they make a mistake their brain grows. Failure and struggle do not mean that they cannot do math—these are the most important parts of math and learning. I don't value students' working quickly; I value their working in depth, creating interesting pathways and representations. I love student questions and will put these onto posters that I hang on the walls for the whole class to think about.
Math is a very creative subject that is, at its core, about visualizing patterns and creating solution paths that others can see, discuss, and critique.
To run a participation quiz, choose a task for students to work on in groups, then show them the ways of working that you value.
Once you have shown these to students, you can start them working. As they work together in groups, walk around the room watching group behavior, writing down comments.
As you circulate and take notes, quote students' actual words when they are noteworthy.
But it is even more important to communicate positive beliefs and expectations to students who are slow, appear unmotivated, or struggle. It is also important to realize that the speed at which students appear to grasp concepts is not indicative of their mathematics potential (Schwartz, 2001).
The most productive classrooms are those in which students work on complex problems, are encouraged to take risks, and can struggle and fail and still feel good about working on hard problems.
We must also resist valuing “effortless achievement”—praising students who are fast with math. Instead, we should value persistence and hard thinking.
When students fail and struggle it does not mean anything about their math potential; it means that their brains are growing, synapses are firing, and new pathways are being developed that will make them stronger in the future.
Instead of saying “You are so smart,” it is fine to say to students something like “It's great that you have learned that,” or “I love how you are thinking about the problem.”
My undergraduates have really worked on this and now praise people for having good thinking and for being accomplished, learned, hard working, and persistent.
There is always some logic in students' thinking, and it is good to find it, not so that we avoid the “failure” idea, but so that we honor students' thinking.
I recently read about a second-grade teacher, Nadia Boria, who offers this response to students when they ask for help: “Let's think about this for a minute. Do you want my brain to grow or do you want to grow your brain today?” (Frazier, 2015).
Mathematics tasks should offer plenty of space for learning. Instead of requiring that students simply give an answer, they should give students the opportunity to explore, create, and grow.
Open up math tasks:
- Instead of asking students to answer the question 1/2 divided by 1/4, ask them to make a conjecture about the answer to 1/2 divided by 1/4 and make sense of their answer, including a visual representation of the solution. As I described in Chapter Five , when Cathy Humphreys asked students to solve 1 ÷ 2/3 she started by saying, “You may know a rule for solving this question, but the rule doesn't matter today, I want you to make sense of your answer, to explain why your solution makes sense.”
- Instead of asking students to simplify 1/3(2x + 15) + 8, a common problem given in algebra class, ask students to find all the ways they can represent that are equivalent.
- Instead of asking students how many squares are in the 100th case, ask them how they see the pattern growing, and to use that understanding to generalize to the 100th case
Ask students to discuss:
- Ways of seeing the mathematics
- Ways of representing ideas
- The different pathways through the problem and strategies
- The different methods used: “Why did you choose those methods? How do they work?”
Encourage students to propose different methods to solve problems and then ask them to draw connections between methods, discussing for example, how they are similar and different or why one method may be used and not another. This could be done with methods used to solve number problems, such as those shown in Figure 5.1 , in Chapter Five .
Ask students to draw connections between concepts in mathematics when working on problems.
In my own teaching of mathematics, I encourage student creativity by posing interesting challenges and valuing students' thinking. I tell students I am not concerned about their finishing math problems quickly; what I really like to see is an interesting representation of ideas, or a creative method or solution. When I introduce mathematics to students in this way, they always surprise me with their creative thinking.
Teachers can encourage students to use intuition with any math problem simply by asking them what they think would work, before they are taught a method.
The teacher provocatively took the students' ideas and made incorrect statements for the students to challenge, and the class considered together all of the possible relationships of angles that preserve the definitions.
In the lesson in China, the teacher did not ask complete-this-sentence questions; she listened to students' ideas and made provocative statements in relation to their ideas that pushed forward their understanding. Her statements caused the students to respond with conjectures and reasons, thinking about the relationships between different angles.
If you give students the opportunity to extend problems, they will almost always come up with creative and rich opportunities to explore mathematics in depth, and that is a very worthwhile thing for them to do.
He points out that students currently spend 80% of the time they spend in math classrooms performing calculations, when they should instead be working on the other three parts of mathematics—setting up models, refining them, and using them to solve real problems.
In my own teaching experience, when I have asked students in classrooms to consider a situation and pose their own question, they have become instantly engaged, excited to draw on their own thinking and ideas. This is an idea for math classrooms that is very easy to implement and needs to be used only some of the time. Students should be able to experience this in school so that they are prepared to use it later in their mathematical lives.
It is so important that employees describe their mathematical pathways to others, in teams, because others can then use those pathways in their own work and investigations and can also see if there are errors in thinking or logic. This is the core of mathematical work; it is called reasoning.
When students act as a skeptic, they get an opportunity to question other students without having to take on the role of someone who doesn't understand.
Tags:
#Blaugust,
Book Excerpts
8.02.2016
Mathematical Mindsets: The Highlights {Part 4}
This book I would say has changed my thoughts on math, teaching, and teaching math more than any other I've read in my seven year career. I will recommend it and link it forever. I will have to post my highlighted notes from it in several posts because no one would ever scroll through all of it otherwise! There is just so much to process and that I will need to read over and over again- so many opportunities for growth and change!
It's only $10.71 for the paperback and $7.99 for the Kindle version. You NEED this book. But until you get your own, this should be enough to make you want more.
Enjoy!
Part 1 {here}
Part 2 {here}
Part 3{here}
Mathematical Mindsets: Unleashing Students' Potential through Creative Math, Inspiring Messages and Innovative Teaching
Jo Boaler
Chapter 7: From Tracking to Growth Mindset Grouping
The strong messages associated with tracking are harmful to students whether they go into the lowest or highest groups (Boaler, 1997; Boaler, 2013a; Boaler & Wiliam, 2001; Boaler, Wiliam, & Brown, 2001).
In the Third International Mathematics and Science Study, for example, the United States was found to have the greatest variability in student achievement—that is, the most tracking. The country with the highest achievement was Korea, which was also the country with the least tracking and the most equal achievement. The United States also had the strongest links between achievement and socioeconomic status, a result that has been attributed to tracking (Beaton & O'Dwyer, 2002). Countries as different as Finland and China top the world in mathematics performance, and both countries reject ability grouping, teaching all students high-level content.
They found that the students who worked without advanced classes took more advanced math, enjoyed math more, and passed the state test in New York a year earlier than students in tracks. Further, researchers showed that the advantages came across the achievement spectrum for low-and high-achieving students (Burris, Heubert, & Levin, 2006). These findings have been repeated in study after study (see, for example, Boaler, 2013b). A substantial body of research points to the harmful effects of tracking, yet the practice is used in most schools across the country.
Most of the unmotivated and bad behavior that happens in classrooms comes from students who do not believe that they can achieve.
In all of my experience teaching heterogeneous groups of students, I have found that when students start to believe they can achieve, and they understand that I believe in them, bad behavior and lack of motivation disappear.
They discovered that when they gave open tasks, all students were interested, challenged, and supported. Over time the students they thought of as low-achieving started working at higher levels, and the classroom was not divided into students who could and students who could not; it was a place full of excited students learning together and helping each other.
The choice or the challenge must always be available to all students.
A one-dimensional math class, of which there are many in the United States, is one in which one practice valued above all others—usually that of executing procedures correctly.
In a multidimensional math class, teachers think of all the ways to be mathematical. No one is good at all of these ways of working, but everyone is good at some of them.
A stunning 97% of students from the traditional approach said the same thing: “Pay careful attention.” This is a passive learning act that is associated with low achievement (Bransford, Brown, & Cocking, 1999).
In the Railside classes, when we asked students the same question, they came up with a range of ways of working, such as:
- Asking good questions
- Rephrasing problems
- Explaining
- Using logic
- Justifying methods
- Using manipulatives
- Connecting ideas
- Helping others
A student named Rico said in an interview, “Back in middle school the only thing you worked on was your math skills. But here you work socially and you also try to learn to help people and get help. Like you improve on your social skills, math skills, and logic skills” (Railside student, year 1).
Another student, Jasmine, added, “With math you have to interact with everybody and talk to them and answer their questions. You can't be just like ‘Oh here's the book, look at the numbers and figure it out.’” When we asked, “Why is that different for math?” she said, “It's not just one way to do it. It's more interpretive. It's not just one answer. There's more than one way to get it. And then it's like: ‘Why does it work?’” (Railside student, year 1).
A theme of the algebra course, and then later all the courses in the school, was multiple representations—students were frequently asked to represent their ideas in different ways, such as through words, graphs, tables, symbols, and diagrams. Students were also encouraged to color code, representing ideas in the same color—for example, using the same color for the x in an expression, diagram, graph, table, and paragraph (see Exhibit 7.4 ).
Many more students were successful because there were many more ways to be successful.
Although the standardized state tests the students had to take under the State of California requirements did not value multidimensional mathematics, the students achieved at high levels because they had learned to be successful in class and to feel good about mathematics. They also approached the state tests as confident problem solvers willing to try any question.
Students were able to get started through encouraging each other, rereading questions, and asking each other questions.
What is the question asking us?
How could we rephrase this question?
What are the key parts of the problem?
But teachers frequently need to inject a new piece of information or a new direction into the group work. In complex instruction, teachers do not try to do this by quieting the whole class. Instead, they call the recorder/reporters out to join the teacher for a huddle. The recorder/reporters meet as a group with the teacher, who can give information that each recorder/reporter takes back to the groups. This not only helps the teacher but also gives the students responsibility that is intrinsically valuable in helping them feel empowered mathematically.
An interesting and subtle approach recommended in the complex instruction pedagogy is that of assigning competence . This practice involves teachers' raising the status of students who they think may be lower status in a group—by, for example, praising something they have said or done that has intellectual value, and bringing it to the group's or the whole class's attention. For example, teachers may ask a student to present an idea or publicly praise a student's work in a whole class setting.
An activity I always like groups to work on before introducing any math work is to ask them to discuss together the things they do and don't like other group members to do and say when they are working in a group on math.
I find that when students think for themselves about positive and negative group discussions and come up with their own lists, they are more thoughtful about the ways they interact in groups.
I also start classes by explaining to students what is important to me. I say that I do not value speed or people racing through math; I value people showing how they think about the math, and I like creative representations of ideas.
Yet another way the Railside teachers encouraged group responsibility is a method that is shocking to some, but that really communicates the idea that group members are responsible for each other. Occasionally the teachers gave what they called “group tests.” Students would take the test individually, but the teachers would take in only one test paper per group (randomly chosen) and grade it. That grade would then be the grade for all the students in the group. This was a very clear communication to students that they needed to make sure all of their group members understood the mathematics.
As the approach they experienced became more multidimensional, they came to regard each other in more multidimensional ways, valuing the different ways of seeing and understanding mathematics that different students brought to problems.
Many parents worry about high achievers in heterogeneous classes, thinking that low achievers will bring down their achievement, but this does not usually happen. High achievers are often high achievers in the U.S. system because they are procedurally fast. Often these students have not learned to think deeply about ideas, explain their work, or see mathematics from different perspectives because they have never been asked to do so. When they work in groups with different thinkers they are helped, both by going deeper and by having the opportunity to explain work, which deepens their understanding. Rather than groups being lowered by the presence of low achievers, group conversations rise to the level of the highest-thinking students. Neither the high nor the low achievers would be as helped if they were grouped only with similar achieving students.
Two practices I have come to regard as particularly important in promoting equity, and that were central to the responsibility students showed for each other, are justification and reasoning.
Always give help when needed, always ask for help when you need it.
Chapter 8: Assessment for a Growth Mindset
Students with no experience of examinations and tests can score at high levels because the most important preparation we can give students is a growth mindset, positive beliefs about their own ability, and problem-solving mathematical tools that they are prepared to use in any mathematical situation.
Study after study shows that grading reduces the achievement of students.
The students receiving comments learned twice as fast as the control group, the achievement gap between male and female students disappeared, and student attitudes improved.
When we give assessments to students, we create an important opportunity. Well-crafted tasks and questions accompanied by clear feedback offer students a growth mindset pathway that helps them to know that they can learn to high levels and, critically, how they can get there.
I have seen this shift happen with many teachers with whom I have worked. It comes about when teachers are treated as the professionals they are and are invited to use their own judgment, helped by research ideas, to create positive learning and assessment experiences for their students.
He went on to describe how the valuing of different mathematics strategies allowed him to feel he could work with mathematics in any way he wanted, to explore ideas and learn about numbers.
When students are given scores that tell them they rank below other students, they often give up on school, deciding that they will never be able to learn, and they take on the identity of an underperforming student.
The grades and scores given to students who are high achieving are just as damaging. Students develop the idea that they are an “A student” and start on a precarious fixed mindset learning path that makes them avoid harder work or challenges for fear that they will lose their A label. Such students often are devastated if they get a B or lower, for any of their work.
When students develop interest in the ideas they are learning, their motivation and their achievements increase.
They found something amazing: a form of assessment so powerful that if teachers shifted their practices and used it, it would raise the achievement of a country, as measured in international studies, from the middle of the pack to a place in the top five.
In A4L, students become knowledgeable about what they know, what they need to know, and ways to close the gap between the two. Students are given information about their flexible and growing learning pathways that contributes to their development of a growth mathematics mindset.
One important principle of A4L is that it teaches students responsibility for their own learning.
Assessment for learning can be thought of as having three parts: (1) clearly communicating to students what they have learned, (2) helping students become aware of where they are in their learning journey and where they need to reach, and (3) giving students information on ways to close the gap between where they are now and where they need to be (see Figure 8.3 ).
The researchers concluded that a large part of the students' previous low achievement came not from their purported lack of ability but from the fact that previously they had not known what they should really be focusing upon.
The two main strategies for helping students become aware of the math they are learning and their broader learning pathways are self-and peer assessment.
If students start each unit of work with clear statements about the mathematics they are going to learn, they start to focus on the bigger landscape of their learning journeys—they learn what is important, as well as what they need to work on to improve.
Studies have found that when students are asked to rate their understanding of their work through self-assessment, they are incredibly accurate at assessing their own understanding, and they do not over-or underestimate it (Black et al., 2002).
In addition to receiving the criteria, students need to be given time to reflect upon their learning, which they can do during a lesson, at the end of a lesson, or even at home.
Peer assessment is a similar strategy to self-assessment, as it also involves giving students clear criteria for assessment, but they use it to assess each other's work rather than their own. When students assess each other's work they gain additional opportunities to become aware of the mathematics they are learning and need to learn.
Peer assessment has been shown to be highly effective, in part because students are often much more open to hearing criticism or a suggestion for change from another student, and peers usually communicate in ways that are easily understood by each other.
When students are given information that communicates clearly what they are learning, and they are asked, at frequent intervals, to reflect on their learning, they develop responsibility for their own learning.
An effective way for students to become knowledgeable about the ideas they are learning is to provide some class time for reflection. Ask students at the end of a lesson to reflect using questions such as those in Exhibit 8.4.
As I noted in Chapter Four, brain science tells us that the most powerful learning occurs when we use different pathways in the brain.
They tell us that mathematics learning, particularly the formal abstract mathematics that takes up a lot of the school curriculum, is enhanced when students are using visual and intuitive mathematical thinking, connected with numerical thinking.
In this realm there is one method that stands above all others in its effectiveness: the process of teachers giving students diagnostic comments on their work. One of the greatest gifts you can give to your students is your knowledge, ideas, and feedback on their mathematical development, when phrased positively and with growth messages.
Always allow students to resubmit any work or test for a higher grade
Share grades with school administrators but not with the students.
Use multidimensional grading.
Do not use a 100-point scale.
Do not include early assignments {review?} from math class in the end-of-class grade .
Do not include homework, if given, as any part of grading.
Tags:
#Blaugust,
Book Excerpts
Subscribe to:
Posts (Atom)